Закону двойного отрицания («отрицания отрицания») посвящена довольно обширная литература с самыми различными точками зрения на него, часто диаметрально противоположными. Однако следует признать, что во многих явлениях и процессах можно в явном виде выделить действие указанного диалектического закона.
Общепринятой стала точка зрения, приводимая в отечественных учебниках философии (А.М. Минасян, 1991; Ю.А. Харин с соавт., 2002; Э.Ф. Звездкина с соавт.; и др.), согласно которой закон двойного отрицания характеризует развитие с позиций его направленности и результата. Диалектическое отрицание предполагает уничтожение только части свойств объекта, которые стали не нужными. При этом сохраняются полезные свойства, а также появляются принципиально новые свойства, что определяет возможность скачкообразного перехода. Согласно этому закону, развитие есть процесс, состоящий из определённых циклов. Значимую роль в принципе диалектического отрицания, как подчеркивает А.М. Минасян, имеет понятие триады (от греч. trias – тройственность), характеризующее динамическую трехступенчатость (или трехфазность) процесса развития.
Обобщая диалектико-материалистические взгляды на триаду, можно констатировать следующие теоретические положения [1, 2, 3]:
1) триада («троичный цикл») объективно имеет место при развитии реальных объектов и явлений;
2) триада развития в общем случае включает следующие звенья: «исходное положение» – «первое отрицание» – «второе отрицание», являющееся «как бы» возвратом к исходному положению на другом (новом, более высоком) уровне;
3) триада характеризует не «механическое» повторение внутри себя или пройденного пути, а поступательное движение. В триаде последнее звено сходно с первым звеном лишь по форме, но по содержанию не совпадает с ним, поскольку оно обогащено новыми приобретениями;
4) триада характеризует цикличность развития и его бесконечность: за первой триадой следует вторая триада, за второй – третья и т.д.; каждый цикл «отрицания отрицания» является, одновременно, результатом предыдущего развития и началом для дальнейшего развития, для новых отрицаний, для разрешения новых противоречий в новых явлениях и в новых условиях.
На указанных теоретических положениях будем основываться при наших дальнейших рассуждениях.
Цель данной работы – показать на различных примерах, что возможны, по крайней мере, две формы связи триад. При этом не ставится задача подробного анализа приведенных примеров в подтверждение закона двойного отрицания: предполагается ясной их (т.е. приводимых примеров) подчиненность этому закону.
Далее для общности все три части триады будем называть звеньями: «исходное положение» – первое, или начальное, звено; «первое отрицание» – второе, или среднее, звено; «второе отрицание» – третье, или конечное, звено.
Первая форма триад известна: назовем ее последовательными триадами.
Например, чередование поколений в органическом мире представляет собой последовательные триады. То же можно отметить в Периодической системе элементов Д.И. Менделеева в виде повторяемости свойств элементов. В математике последовательное перемножение на отрицательную величину тоже создают последовательные триады; это обстоятельство обычно показывается в математическом выражении через сомножитель (-1)n.
В последовательных триадах всегда третье звено, т.е. второе отрицание, является первым звеном (исходным положением) – для следующей триады.
Подобный «троичный цикл» в форме последовательных триад характерен, в основном, для развития объектов (или явлений), имеющих два устойчивых полярных состояния, например, два противоположных научных тезиса, две полярных свойства и т.д. В простейших случаях имеет место отрицание как «переход в свою противоположность» уже в соседних звеньях, а в результате их синтеза получаем триаду.
Последовательные триады можно изобразить графически, взяв некую плоскую спираль. Для этого есть достаточные основания. Двойное отрицание («отрицание отрицания») представляет ситуацию «как бы возврата» к старому: объект или явление превращается в свое отрицание (первая фаза); потом опять происходит отрицание (вторая фаза); в результате третья фаза имеет формальное сходство с первой. Если бы имело место точное совпадение свойств конечного звена со свойствами начального (что характеризует отсутствие развития), то изменение шли бы по кругу. При наличии восходящего движения объект возвращается «как бы» к исходному состоянию, но на другом, более высоком уровне. Поэтому о диалектическом развитии говорят как о движении по спирали. По сути, спираль, характеризующая развитие, объединяет в себе свойства круга и прямой линии.
В качестве иллюстрации возьмем наиболее простую спираль Архимеда (рисунок 1).
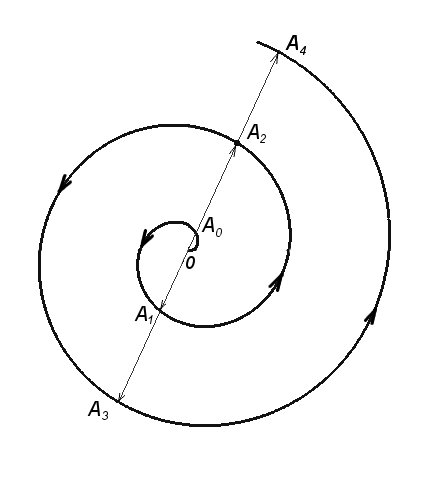
Рисунок 1 - Иллюстрация последовательных триад: Спираль Архимеда и секущая прямая – «линия отрицания»
Через полюс (точка О) спирали под любым углом проведем произвольную секущую прямую линию, которую назовем «линией отрицаний». Последовательные точки пересечения этой прямой со спиралью будем считать обозначающими взаимно отрицающие состояния. Таким образом, исходное состояние, характеризуемое точкой А0, «отрицается» состоянием в точке А1 («переход в свою противоположность») состояние; в точке А1 отрицается состоянием в точке А2, которое является, как бы, «возвратом» к состоянию в точке А0 , но уже на «высшем уровне», т.к. по крайней мере ее радиус-вектор больше радиус-вектора точки А0. Состояние в точке А2 , в свою очередь, является исходным состоянием для следующей триады и отрицается состоянием, характеризуемым точкой А3, которое затем отрицается состоянием, описываемым точкой А4 и т.д.
Заметим, что проведенная на рисунке 1 прямая «линия отрицаний» не имеет никакого преимущества перед бесконечным множеством других возможных прямых «линий отрицания», и рисунок 1 – это только приближенная иллюстрация последовательных триад.
Р.Ф. Абдеев отмечал, что в сложных информационных структурах, характеризующихся самоорганизацией, действие закона двойного отрицания может проявляться иначе, чем в простых объектах, имеющих лишь противоположных состояния. Здесь число переходов может быть более трех, причем объект в ходе диалектического отрицания переходит не сразу в свою противоположность, а прежде попадает на промежуточный, но более высокий уровень организации, характеризующийся качественно новым состоянием [4]. Нам представляется, что в этом случае, когда среднее звено триады усложнено, оно может разворачиваться в виде внутренней (вложенной) триады.
Соответственно, вторую форму связи триад назовем вложенными триадами – здесь отдельные триады как бы вложены одна в другую. Известные примеры из философской классики: 1) смены общественных формаций: «первобытный коммунизм» – «классовое общество» – «коммунистическое общество (научный коммунизм)». Внутри этой триады вложена триада классового общества: «рабовладение» – «феодализм» – «капитализм», которые совместно тоже образуют двойное отрицание. У капитализма есть ряд черт, сближающих его с рабовладельческим обществом. Капитализм, особенно государственно- монополистический, по представлениям классиков марксизма, является чем-то вроде коллективного рабовладельца.
Ф. Энгельс, иллюстрируя в работе «Анти-Дюринг» закон «отрицания-отрицания», пишет о насекомых: «Они развиваются из яичка путем отрицания его, проходят через различные фазы превращения до половой зрелости, спариваются и вновь отрицаются, т.е. умирают, как только завершился процесс воспроизведения и самка отложила множество яиц» [5, с. 140]. Все эти различные фазы превращения у насекомых с полным циклом развития тоже образуют триаду. В триаде «насекомое – промежуточное звено – насекомое» у высших насекомых промежуточное звено образует (внутреннюю) триаду: «яичко» – «личинка» – «куколка», где «куколка» является своеобразным возвратом к стадии «яичко».
Следующий пример возьмем из математического анализа, где высшие производные (дифференциалы) и кратные интегралы тоже образуют вложенные триады. В триаде «функция» – «производная» – «интеграл» среднее звено может быть усложненным, имея высшие производные. Тогда низшая производная, будучи исходной, отрицается следующей за ней по порядку высшей производной, что влечет за собой появление соответствующего интеграла. В математике в виде вложенных триад могут выступать также логарифмы.
Из приведенных примеров на вложенные триады можно сделать следующий вывод:
Вложенные триады появляются всегда, когда среднее звено данной триады усложняется; оно (это звено) – с необходимостью – разворачивается во внутреннюю (вложенную) триаду.
Среднее звено вложенной триады тоже может усложниться, и тогда оно тоже, – с необходимостью, – развернется уже во вторую вложенную триаду, по отношению к которой первая окажется внешней. Этот процесс может продолжаться и дальше. Трехступенчатостью завершается данный цикл развития, но не само развитие. Развитие, в общем случае, бесконечно, и каждый цикл «отрицания отрицания» является, одновременно, результатом и началом – началом, новой исходной точкой для дальнейшего развития, для новых отрицаний.
Трудно сказать, могут ли разворачиваться в свои особые триады крайние звенья данной триады. Однако пренебрегать такой возможностью нельзя, пока не будет показано обратное.
На рисунке 2 приводится графическая иллюстрация вложенных триад.
На рисунке 2 условно показана одна вложенная триада в виде годографа, представляющего некую спиралевидную кривую. Далее в наших рассуждениях для краткости будем называть состояние словом «точка» (с соответствующим индексом), имея в виду точки на рисунке 2, характеризующие определенные состояния рассматриваемого объекта или явления.
Примем за исходное состояние точку А0. Это состояние «отрицается» точкой А1, которое в свою очередь, является исходным состоянием для вложенной триады и «отрицается» точкой А’1. Состояние в точке А1‘ отрицается точкой А”1, являющейся, как бы, «возвратом» к состоянию в точке А1 – и на этом заканчивается вложенная триада. Далее «отрицается» состояние, в точке А”1 или, иначе, «отрицается» в целом вложенная триада новым состоянием, описываемое точкой А2 внешней триады, где точка А1 является, как бы, «возвратом» к исходному состоянию (точке А0), но на новом уровне.
На рисунке 2 вложенная триада имеет свой особый полюс О’1 по отношению к внешней триаде. Если не будет доказано обратное, можно предполагать также возможность совмещения полюсов (точек О и О’1).
В общем случае взаимно-отрицающее точки (состояния), при изображении их графически на плоскости, не обязательно должны быть расположены на одной прямой: угол («раствор») между ними может и отличаться от 1800. Точно также полюсы О и О’1 не обязательно должны располагать на одной прямой с взаимно-отрицающими («полярными») точками, как это показано на рисунке 2.
Выше уже отмечалось, что при первой форме триад («последовательные триады») их последовательность циклов образует явную спираль (рис. 1). Обратим внимание на то, что и то при второй форме триад («вложенные триады»), последовательность их циклов в совокупности образует спиралевидную кривую, имеющий выраженный немонотонный (с возвратами, колебаниями) характер.
Почему развитие можно представлять происходящим по спирали, или, точнее, спиралевидной кривой? В пользу спиралевидности обобщенной траектории развития Э.Ф. Звездкина с соавторами приводит ряд доводов, с которыми нельзя не согласиться [3]. Кратко сформулируем их:
1) Спираль иллюстрирует развитие в виде сложного нелинейного, в том числе немонотонного процесса, имеющего зигзаги, временные возвраты на более низкую ступень развития, ветки развития с признаками неустойчивости с последующим саморазрушением, – и все это при доминирующей тенденции глобального восходящего процесса;
2) Образ спирали позволяет рассматривать цикл развития как «виток», включающий ряд прошлых фаз, выражающих и деградацию, и созидание. Возврат к старому не означает полного повторения фазы или ступени развития. В целом образ спирали иллюстрирует направленность прогрессивного развития – через смену качества, разрешение противоречий, синтез нового при отрицании старого.
Считаем необходимым привести еще один довод в пользу спиралевидного развития. Развитие по спирали происходит еще и потому, что в спиралях нет симметрии. Но в них скрывается возможность симметрии (зеркальной, центральной). Собственно, сам закон «отрицания отрицания» – несимметричен. И если он и применим для «симметричных» явлений, то только потому, что эти явления представляют собой частный случай асимметрии. Симметрия относительна, а асимметрия абсолютна; симметрия может рассматриваться как «частный случай» асимметрии.
По-видимому, вложенная триада не только позволяет усложнить конечное звено внешней триады, но и создает возможность для объекта (явления) выйти на какой-то еще более высокий уровень развития, к которому она – эта вложенная триада – имеет отношение. А это уже будет скачок, перерыв постепенности, более значительный, чем простая триада.
Можно установить зависимость числа звеньев от числа триад для обеих рассмотренных выше форм связи: последовательных и вложенных триад (таблица 1).
Таблица 1 – Зависимость числа звеньев от числа вложенных триад
| Число вложенных триад (n) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
| Число звеньев (p) |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
… |
Отсюда, число звеньев в зависимости от числа вложенных триад может быть определено по следующей формуле
Р = 2*n + 1,
где n – число триад, р – общее число звеньев. Таким образом, каждая новая триада добавляет два звена.
В природе обе указанные формы связи триад могут существовать одновременно, «пересекаться» друг с другом, т.е. в одном и том же процессе наряду с одной формой связи может быть другая. Но умение их выделять, различать дает возможность более точно устанавливать направление исследований того или иного объекта, явления или процесса. В этом смысле важную значимость приобретают так называемые «вложенные триады», рассмотренные в данной статье. Выделение и распознавание в реальной действительности этой формы связи триад во многих случаях укажет на действие закона «отрицания отрицания» там, где оно раньше не усматривалось или усматривалось довольно смутно.
Закон «отрицания отрицания» выражает преемственность, спиралевидность развития, связь нового со старым, своего рода повторяемость на высшей стадии развития некоторых свойств ряда низших стадий, обосновывает прогрессивный характер развития.
Время перехода от одного отрицания – к другому (а также от одного цикла – к следующему) во многом определяется внешними условиями. Но в первую очередь это время зависит от действия двух других законов диалектики – закона «единства и борьбы противоположностей» и закона «перехода количественных изменений в качественные».
Диалектический закон двойного отрицания имеет всеобщее значение. Он проявляется во всех сферах объективной реальности – в растительном и животном мире, в геологии, математике, истории, философии, психологии.
Библиографический список
- Минасян А.М. Диалектика как логика. Учебник по философии. Ростов-на-Дону: РИСИ, 1991. 536 с;
- Харин Ю.А. (ред.) Философия: Учеб. пособие для студентов вузов /В.Ф. Берков, П.А. Водопьянов, Е.З. Волчек и др. Под общ. ред. Ю.А. Харина. 3-е изд., доп. и испр. Мн.: ТетраСистемс, 2002. 416 с.
- Звездкина Э.Ф., Егоров В.Ф. Теория философии : Учебное пособие / Научн. ред.: Л.П. Буева. – М.: Филол. о-во СЛОВО; Изд-во Эксмо, 2004. 448 с.
- Абдеев Р.Ф. Философия информационной цивилизации. М.: ВЛАДОС, 1994. 336 с.
- Энгельс Ф. Анти-Дюринг. Переворот в науке, произведённый господином Евгением Дюрингом // Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 20.

