В данной статье остановимся на отдельных вопросах формирования индивидуального теста при построении оптимальной траектории обучения в личностно ориентированной обучающей системе [1, 2]. Актуальность данных вопросов основана на использовании критериально-ориентированных индивидуальных тестов как фундаментальной базы применения системы индивидуального тестирования [3, 4]. Такие тесты позволяют в автоматизированных информационно-образовательных программных средах [5, 6] реализовать различного рода алгоритмы математического моделирования учебных ситуаций при изучении предметного материала [7, 8, 9].
Формирование индивидуального теста возможно по разным темам различных математических дисциплин [10, 11]. В тех случаях, когда материал темы представлен сложной графовой моделью, необходимо разбить данный граф на подграфы, для вершин которого полустепень захода не превышает 1. Такое разбиение объясняется логикой изучения данного материала [12, 13]. Выделение завершенных и самостоятельных частей позволяет выяснить причины возникновения ошибок у учащихся при выполнении тестовых заданий с целью дальнейшей коррекции полученных ими знаний. Затем для каждого из подграфов применяется процесс формирования критериально-ориентированного индивидуального теста [14].
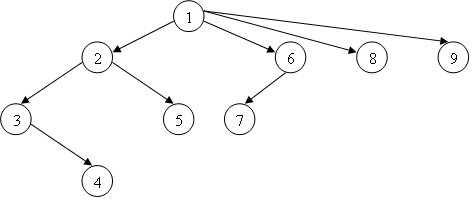
При формализации области изучаемой дисциплины встречаются как графовые модели подобные модели, приведенной на рисунке 1 (дерево, полустепень захода вершин не более 1), так и графы с более сложной структурой (полустепень захода вершин более 1). Приведем такие примеры.
Рисунок 1 – Графовая модель G изучаемого материала
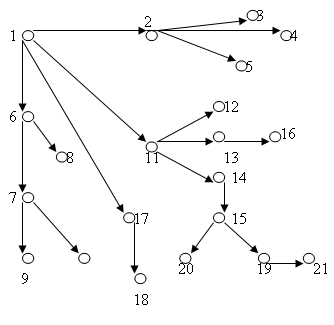
На рисунке 2 приведен пример графовой модели материала темы «Квадратные уравнения», полустепень захода вершин не более 1.
Рисунок 2 – Графовая модель теоретического материала по теме «Квадратные уравнения»
В данной модели вершинам графа соответствуют следующие элементы знания:
1 – определение квадратного уравнения;
2 – уравнение вида x2 = d;
3 – d > 0 – два действительных корня;
4 – d = 0 – корень 0;
5 – d < 0 – нет действительных корней;
6 – неполные квадратные уравнения;
7 – уравнение вида ax2 + c = 0;
8 – уравнение вида ax2 + bx = 0, b ≠ 0;
9 – c < 0 – два действительных корня;
10 – c = 0 – корень 0;
11 – метод выделения полного квадрата;
12 – b2 – 4ac < 0 – действительных корней нет;
13 – b2 – 4ac = 0 – один действительный корень;
14 – формула корней квадратного уравнения;
15 – b2 – 4ac > 0 – два действительных корня;
16 – формула корней квадратного уравнения;
17 – формула корней приведенного квадратного уравнения;
18 – теоремы Виета (прямая и обратная);
19 – формула корней уравнения ax2 + 2mx + c = 0;
20 – определение квадратного трехчлена;
21 – формула разложения на множители.
На рисунке 3 приведен пример графовой модели материала темы «Квадратичные функции», полустепень захода вершин более 1.
Рисунок 3 – Модель теоретического материала по теме «Квадратичные функции»
В приведенной модели вершинам графа соответствуют следующие элементы знания:
1 – определение квадратичной функции;
2 – нули квадратичной функции;
3 – функция у = x2;
4 – свойства;
5 – интервалы знакопостоянства;
6 – четность, симметричность графика;
7 – монотонность;
8 – экстремум;
9 – функция у = ax2;
10 – функция y = ax2 + bх + c;
11 – график функции;
12 – вид и расположение графика в зависимости от коэффициентов;
13 – выделение полного квадрата;
14 – формулы координат вершины;
15 – способы построения (по направлению ветвей и характерным точкам, с помощью преобразований графика у = x2);
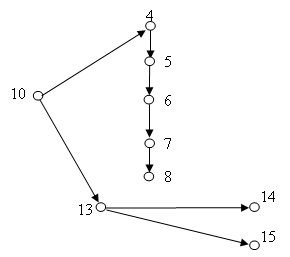
При повторении изученного материала данный граф можно разбить на подграфы, для вершин которого полустепень захода не превышает 1 (см. рис. 4-7). При этом полученные подграфы соответствуют логике разбиения материала и представляют собой инварианты изучаемой темы [15, 16].
На рисунке 4 знания, ассоциированные с вершинами графа, соответствуют введению понятия «квадратичная функция», рассмотрению простейшего примера – функции у = x2 и некоторых ее свойств.
Рисунок 4 – Подграфы по теме «Квадратичные функции»
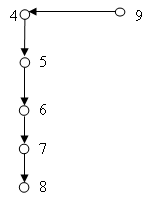
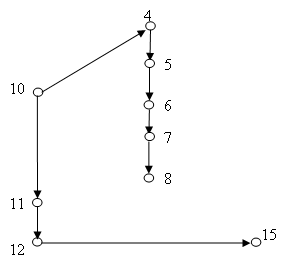
На рисунке 5 знания, ассоциированные с вершинами графа, соответствуют рассмотрению функции у = ax2 и таких свойств этой функции как интервалы знакопостоянства, четность, симметричность графика, монотонность и экстремум. На рисунке 6 – изучению функции y = ax2 + bх + c и ее свойств, а также способов построения графика данной функции на основании выделения полного квадрата. На рисунке 7 – рассмотрению построения графика функции y = ax2 + bx + c на основании изучения ее свойств.
Рисунок 5 – Подграфы по теме «Квадратичные функции»
Рисунок 6 – Подграфы по теме «Квадратичные функции»
Рисунок 7 – Подграфы по теме «Квадратичные функции»
После выполнения первого индивидуального теста для ученика, не справившегося с его заданиями, выделяется новое множество вершин M, и повторяется описанный процесс. Для возможности повторения учебного материала и на индивидуальную помощь каждому ученику необходимо отводить время, соответствующие его личным способностям.
Первый индивидуальный тест может выполняться в рамках времени отведенного на уроке для коррекции знаний, например, работа над ошибками, последующие – в виде самостоятельной работы вне занятий в школе или дома. Если ученик справился с индивидуальным тестом полностью, т.е. устранил свои пробелы в усвоении данного материала, то построение индивидуальной траектории обучения осуществляется в зависимости от его личностного запроса [17, 18].
Таким образом, каждый ученик в зависимости от своих потребностей и возможностей с помощью системы индивидуальных тестовых заданий имеет возможность осуществить свой образовательный запрос [19]. Одновременно с этим, если он достиг в обучении минимально необходимого уровня усвоения учебного материала, то он переходит к изучению следующей темы. Образовательный процесс в этом случае состоит из параллельных действий по времени: изучение нового материала и коррекция предыдущих знаний, с отработкой умений и формированием навыков. Следовательно, обеспечивается, как требует того стандарт обучения, получение учащимися знаний соответствующих минимальному объему содержания образования и обучение идет по оптимальной индивидуальной траектории [20]. В этом случае рационально и эффективно организовать процесс личностно ориентированного обучения возможно с использованием инновационных автоматизированных дидактических систем [21].
Библиографический список
- Козлов С. В. Индивидуальное тестирование в условиях личностно ориентированного обучения // Актуальные проблемы дидактики высшей школы: современные технологии обучения. – Смоленск: СмолГУ, 2007. – Вып. 2. С. 201-211.
- Козлов С. В., Емельченков Е. П. Технология конструирования индивидуального теста в личностно ориентированной обучающей системе // Методология и методика информатизации образования: концепции, программы, технологии: материалы Всероссийской научно-практической конференции 17-19 октября 2005 года. – Смоленск: СГПУ, 2005. – Вып. 2. – С. 39-42.
- Козлов С. В. Тестирование в условиях личностно ориентированного обучения // Методология и методика информатизации образования: концепции, программы, технологии: материалы Всероссийской научно-практической конференции. – Смоленск: СГПУ, 2005. – Вып. 1 – С. 67-75.
- Сенькина Г.Е., Бояринов Д.А., Козлов С. В. Индивидуальное тестирование в личностно ориентированной обучающей системе // Развитие методов и средств компьютерного тестирования: материалы 3-ей Всероссийской научно-методической конференции. – М.: МГУП, 2005. С. 191-194.
- Козлов С. В. Электронный информационно-образовательный ресурс «Advanced Tester» // Хроники объединенного фонда электронных ресурсов «Наука и образование». – 2011. – №11 (30). – URL: http://ofernio.ru/portal/newspaper/ofernio/2011/11.doc.
- Козлов С. В. Система индивидуального тестирования «Комплекс измерения обученности» // Системы компьютерной математики и их приложения. – Смоленск: СмолГУ, 2007. С. 223-225.
- Сенькина Г. Е., Емельченков Е. П., Киселева О. М. Методы математического моделирования в обучении: монография. – Смоленск, 2007. – 112 с.
- Емельченков Е. П., Бояринов Д. А., Козлов С. В. Информационные системы автоматизированной поддержки инновационной деятельности: модели, проектирование и реализация. – Смоленск: Изд-во СмолГУ, 2011. – 164 с.
- Козлов С. В. Особенности применения системы индивидуального тестирования «Комплекс измерения обученности» в школьном курсе информатики // Системы компьютерной математики и их приложения. – Смоленск: СмолГУ, 2008. С. 247-251.
- Козлов С. В. Особенности обучения школьников информатике в профильной школе // Научно-методический электронный журнал «Концепт». – 2014. – № 1. – С. 31-35. ART 14006. – URL: http://e-koncept.ru/2014/14006.htm.
- Козлов С. В. Организация обучения информатике в профильной школе с использованием инновационных образовательных систем // Инфокоммуникационные технологии в региональном развитии: Сборник трудов седьмой ежегодной межрегиональной научно-практической конференции. – Смоленск: СПЭК, 2014. – С.71-73.
- Козлов С. В. Использование математического аппарата теории графов для построения модели предметной области в информационном образовательном пространстве «Средняя школа – ВУЗ» // Инфокоммуникационные технологии в региональном развитии: Сборник трудов четвертой ежегодной межрегиональной научно-практической конференции. – Смоленск: СПЭК, 2011. – С.108-110.
- Козлов С. В. Вопросы проектирования инновационных автоматизированных информационных систем: анализ элементов графовых моделей // Система обеспечения качества образования: модели, технологии, анализ: материалы научно-методической конференции. – Смоленск: Смоленский филиал РГТЭУ, 2012. С. 53-57.
- Емельченков Е. П., Бояринов Д. А., Козлов С. В. Информационное образовательное пространство: модели и технологии: монография / Е. П. Емельченков, Д. А. Бояринов, С. В. Козлов, З. А. Нырцова, А. П. Борисов. – Смоленск, 2010. – 216 с.
- Козлов С. В. Программный комплекс «Advanced Tester»: математические аспекты формирования оптимальных индивидуальных стратегий обучения // Современные информационные технологии в образовании и научных исследованиях (СИТОНИ-2012): материалы III-й международной научно-технической конференции студентов и молодых ученых. – Донецк: ДонНТУ, 2012. – С. 223-226.
- Киселева О. М. Использование математических методов для формализации элементов образовательного процесса // Концепт. – 2013. – № 02 (февраль). – ART 13001. – 0,4 п. л. – [Электронный ресурс] – URL: http://e-koncept.ru/2013/13032.htm. – Гос. рег. Эл № ФС 77- 49965. – ISSN 2304-120X. – [Дата обращения 09.02.2013].
- Козлов С. В. Педагогическое проектирование индивидуального тестирования в личностно ориентированной обучающей системе: дис. … канд. пед. наук: 13.00.01 и 13.00.02: защищена 24.05.06: утв. 20.11.06 / Козлов Сергей Валерьевич. – Смоленск, 2006. – 204 с.
- Козлов С. В. Педагогическое проектирование индивидуального тестирования в личностно ориентированной обучающей системе: автореферат дис. … канд. пед. наук. – Смоленск, 2006. – 18 с.
- Козлов С. В. Актуальные вопросы использования адаптивных информационно-образовательных систем в профильной школе // Наука и образование в XXI веке: сборник научных трудов по материалам международной научно-практической конференции 30 сентября2013 г.: в 34 частях. – Ч. 21. – Тамбов: Бизнес-Наука-Общество, 2013. – С. 48-51.
- Козлов С. В. Основы применения педагогической технологии индивидуального тестирования для формирования оптимальной траектории обучения // Современные научные исследования и инновации. – 2014. – № 4 (36). – С. 76.
- Козлов С. В. Возможности и особенности построения автоматизированных дидактических систем // Математическая морфология: электронный математический и медико-биологический журнал. – Т. 10. – Вып. 3. – Смоленск: СГМА, 2011.