Одним из характерных признаков больших систем (а именно с ними имеет дело авиационный командир, штаб и любой другой управляющий орган) является огромный поток информации, которую необходимо обрабатывать в процессе принятия решений. Каждый ее элемент вносит дополнительные знания об управляемом объекте и способствует созданию более полной и адекватной модели. С другой стороны, обилие информации занимает много времени на анализ, затрудняет отделение главного от второстепенного, что может привести к ошибочным решениям. Назначение факторного анализа состоит в том, чтобы управляющему органу представить информацию в более сжатой форме, сократив при этом до разумного минимума неизбежные потери в ее содержании. Предпосылки для решения такой задачи видятся во взаимосвязи составляющих информационного потока в том, что они частично перекрывают друг друга. Редки случаи когда, когда какой-то показатель характеризует лишь одну сторону явления и никак не связан с другими. Например, скоростные данные самолета характеризуют его как с точки зрения возможности выполнять заданные задачи в заданные сроки, так и с точки зрения его возможностей по преодолению ПВО противника, они оказывают влияние на маневренность и многое другое [1].
На математическом языке, нами рассматриваются объекты, которые по какой-либо причине (функциональному назначению) могут быть отнесены к определенному классу: боевые средства разных типов, технические средства или группа лиц для выполнения ответственного задания.
Главные цели факторного анализа: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных [2,3].
Процесс выделения факторов начинается в составления матрицы коэффициентов корреляции, определенных в результате эксперимента. Цель состоит в переходе от редуцированной матрицы корреляции к редуцированной факторной матрице, которая позволит определить необходимое число факторов и каковы нагрузки каждого фактора для переменных. Уравнение для некоррелируемых факторов имеет вид:
R = F ∙ F’,
R – матрица корреляций,
F – редуцированная факторная матрица,
F’ – транспонированная факторная матрица [4,6].
В геометрической интерпретации каждый коэффициент матрицы корреляций равен скалярному произведению пары единичных векторов на косинус угла между ними:
R12 = h1 ∙ h2 ∙ cosα12
Методическая разработка, которая представлена на кафедре математики ВУНЦ ВВС «ВВА имени профессора Н. Е. Жуковского и Ю. А. Гагарина» (г. Воронеж) содержит тактико-технические характеристики самолетов для их последующей обработки методами факторного анализа [8-12].
База данных содержит количественные характеристики 57 отечественных самолетов:
- Год принятия на вооружение
- Размах крыльев, м
- Длина самолета, м
- Высота, м
- Площадь крыла, кв.м.
- Максимальная скорость на высоте, км/ч
- Экипаж, чел.
- Масса пустого самолета, кг
- Практический потолок, м
- Практическая дальность, км
На основе этих данных нами были выбраны 4 характеристики, которые, по нашему мнению, являются наиболее показательными и имеют важное дидактическое значение для дальнейшего изучения методов факторного анализа:
- Площадь крыла, кв.м. (далее «Площадь»)
- Максимальная скорость на высоте, км/ч («Скорость»)
- Масса пустого самолета, кг («Масса»)
- Практический потолок, м («Потолок)
На этапе корреляционного анализа прослеживается наличие в структуре данных 2 фактора. Тесно связаны шкалы «Площадь» и «Масса», а также «Потолок» и «Скорость», причем между собой у них связь равна почти нулю.
Таблица 1 – Корреляционная матрица
|
Площадь |
Скорость |
Масса |
Потолок |
||
| Площадь |
1 |
,017 |
,871** |
,026 |
|
|
,903 |
,000 |
,849 |
|||
| Скорость |
,017 |
1 |
,072 |
,835** |
|
|
,903 |
,597 |
,000 |
|||
| Масса |
,871** |
,072 |
1 |
,066 |
|
|
,000 |
,597 |
,626 |
|||
| Потолок |
,026 |
,835** |
,066 |
1 |
|
|
,849 |
,000 |
,626 |
|||
| **. Корреляция значима на уровне 0.01 (2-сторон.). | |||||
На этапе факторизации матрицы с помощью метода главных компонент можем убедиться в наличии двух факторов, «объясняющих» исходные данные (см. Табл.2 и рис.1).
Таблица 2 – Матрица компонент
|
Компонента |
||
|
1 |
2 |
|
| Площадь |
,968 |
-,003 |
| Скорость |
,022 |
,958 |
| Масса |
,966 |
,050 |
| Потолок |
,024 |
,957 |
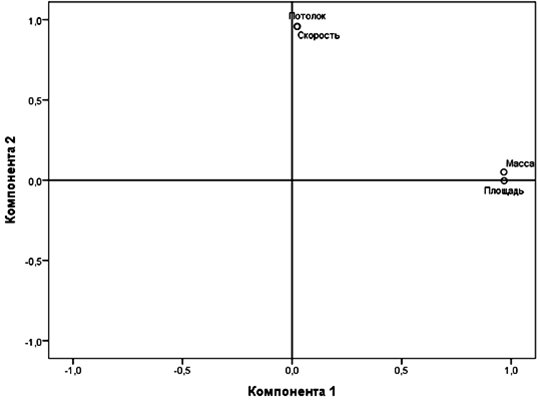
Рис. 1. График компонент в повернутом пространстве
Заключительный этап – интерпретация факторов:
1 фактор – «Технические характеристики» = «Масса» + «Площадь»;
2 фактор – «Летные характеристики» = «Скорость» + «Потолок».
Библиографический список
- Жиров А.Ю., Соболевская З.Т., Тихомирова Э.Ю. Военно-прикладная математика: учебное пособие. Монино, 2010. – 240 с.
- Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. – СПб.: Речь, 2004. – 392 с.
- Суходольский Г.В. Математические методы в психологии / Г.В. Суходольский. – Харьков: Изд-во Гуманитарный Центр, 2006. – 284 с.
- Остапенко Р.И. Основы структурного моделирования в психологии и педагогике: учебное пособие для студентов и аспирантов психологических и педагогических специальностей вузов / Р. И. Остапенко. – Воронеж.: ВГПУ, 2012. – 124 с.
- Остапенко Р.И. Математические основы психологии: учебно-методическое пособие. – Воронеж.: ВГПУ, 2010. – 76 с.
- Остапенко Р.И. Латентное в социо-гуманитарном знании: понятие и классификация // Современные научные исследования и инновации. – 2012. – № 7 (15). – С. 5.
- Остапенко Р.И. Структурное моделирование в науке и образовании: краткий обзор и перспективы развития // Современные научные исследования и инновации. – 2013. – № 9 (29). – С. 30.
- Остапенко Р.И. Методические аспекты формирования информационно-математической компетентности студентов гуманитарных специальностей // Современные научные исследования и инновации. – 2013. – № 5 (25). – С. 29.
- Остапенко Р.И. Формирование математической компетентности студентов-психологов в условиях самодиагностики по курсу «Математические основы психологии» // Перспективы науки и образования. – 2013. – № 6. – С. 91-96.
- Остапенко Р.И. Методические аспекты формирования информационно-математической компетентности студентов гуманитарных специальностей // Современные научные исследования и инновации. – 2013. – № 5 (25). – С. 29.
- Остапенко Р.И. Самодиагностика как условие формирования математической компетентности студентов психологических специальностей // Современные научные исследования и инновации. – 2013. – № 10 (30). – С. 44.
- Остапенко Р.И. Использование структурных уравнений в моделировании процессов управления образованием // Управление образованием: теория и практика. – 2013. – № 4 (12). – С. 1-8.


